
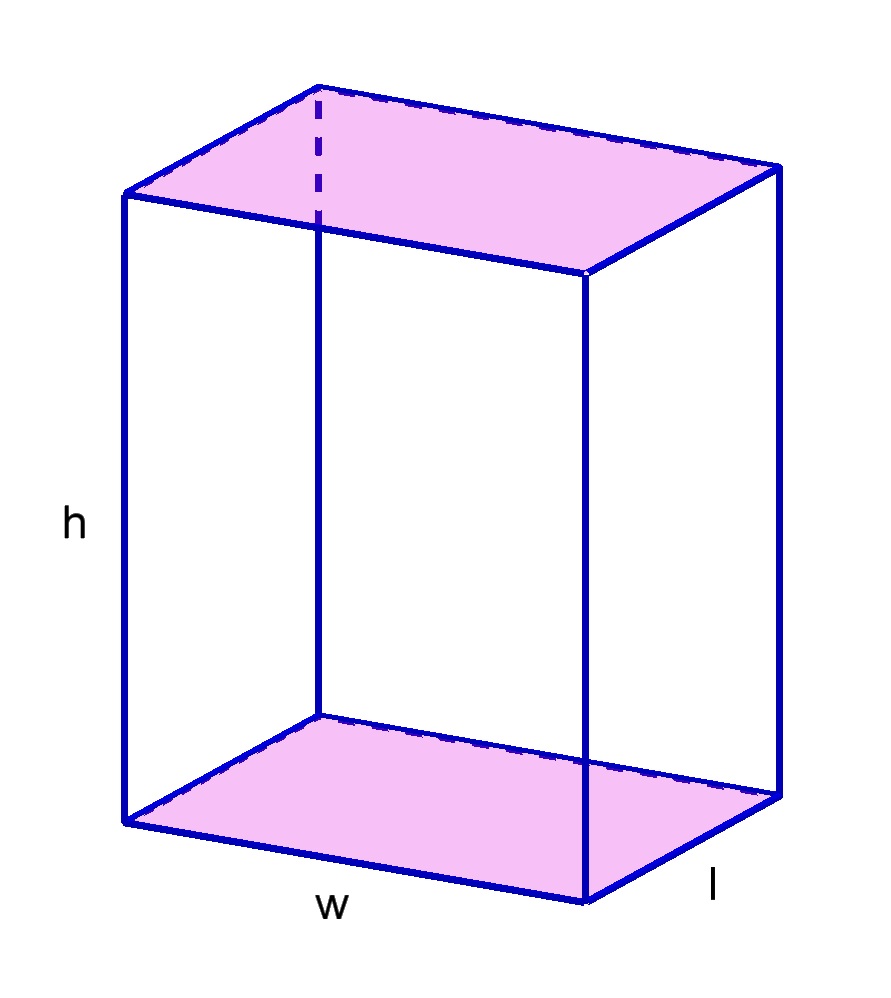

You could have used different axioms, like postulating Cavalieri's principle or the idea of a moving segment (like in calculus, but of constant length).For example, if a rectangular prism is 4 feet long, 2 feet wide and 1.
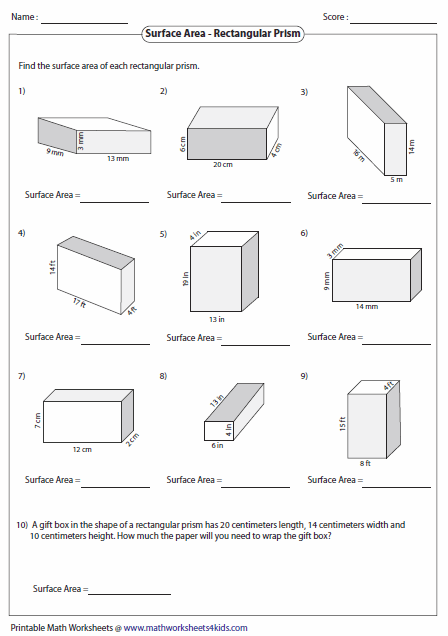
Find the area of a rectangular prism whose length, width, and height are given, respectively. To find the surface area of the entire prism, add those calculations: 2lw + 2lh + 2wh. Prisms are solids with flat parallelogram sides and identical. You probably can find these things in books of Plane Euclidean Geometry, but I don't have any such book, so I can't give you a good indication. The formula to find the area of a rectangular prism is, A 2 (lh +wh + lw ) A 2 (8×4+6×4+8×6) A 2 (32+24+48) A 2 (104) A 208 sq.cm. The surface area of a rectangular prism is the total area or region covered by its six faces.You can just be happy with approximations or use the method of exhaustion (or the theory of limits) to show that the formula is exact. In case 2, we need to find a new unit of length that in commensurable with our original unit of length, and that will take us to the proof in case 1. Then we can prove the formula for the area of the rectangle if we can show that the rectangle is decomposed into ab unit squares. In case 1, let's say the sides are a and b, we divide the sides into parts of unit length and draw the perpendiculars. Theorem: The area of a rectangle is the product of the lengths of its sides.ģ) At least one of the lengths is an irrational number (the Greeks discovered this can happen in geometry as a consequence of the Pythagorean theorem). That's because I don't think I can do more than it right now.ģ) If a simple polygon P is decomposed into a finite number of parts, then the area of P is the sum of the areas of the parts. I assume you mean the areas of three faces of a rectangular prism (or some figure whose volume is length x width x height, a parallelepiped), and that no two of your given sides are opposite one another, so you dont have redundant information. I will give just a sketch for your first question. Anyway, this is how many people initially learned it: If you want a proof in the style of classical geometry (which is the way we usually learn it in school, but without the proofs -haha), it's much harder to check if it is rigorous than an analytic one. Step 2: Draw a net diagram using the given side length. Or take it as a primitive notion and "define" (abuse of language here) it via axioms. Step 1: Identify the given side lengths of a rectangular prism. You need to first define area if you want to prove something about it.


 0 kommentar(er)
0 kommentar(er)
